Templot Club Archive 2007-2020
|
|||
| author | remove search highlighting | ||
|---|---|---|---|
|
posted: 13 Feb 2013 10:14 from: CoBo
click the date to link to this post click member name to view archived images |
Okay... just trying to get my head round frog angles and must point out geometry wasn't my niche subject at school. If my understanding is correct, I think that B, C, D etc, relate to the length of a turnout and that 8, 9, 10, to the amount the diverging track moves away from the main over a given distance, eg a C:10 is a long point where the diverging track moves away from the main at 1cm in every 10cms. I also understand the difference between Right Angle Measurement (RAM) and Centre Line Measurement (CLM). I've seen filing jigs where one can file the frog rails to the required angles eg 10, 12 etc. and assume that all 10's or 12's etc have the angle set the same - I don't mean 10 will be the same as 12 but that all 10's will be the same and all 12's will be the same. Am I therefore correct in believing that all frogs on for instance a B:7 turnout will be exactly the same angle irrespective of turnout shape ie straight or curved? If this is true, have we a list of what these frog angles are - or should be. Or have I got it all wrong - again. |
||
|
posted: 13 Feb 2013 11:23 from: Martin Wynne
click the date to link to this post click member name to view archived images |
CoBo wrote: Am I therefore correct in believing that all frogs on for instance a B:7 turnout will be exactly the same angle irrespective of turnout shape ie straight or curved?Hi Mike, A basic explanation of the REA turnout sizes is on the Templot "Making a Start" page at: http://www.templot.com/martweb/gs_firstoff.htm (I've just noticed that page has two sections, labelled 1 and 3. Yes, all V-crossings (frogs) of the same unit angle are the same angle where the rails intersect at the "fine point" (FP): 2_130719_380000000.png 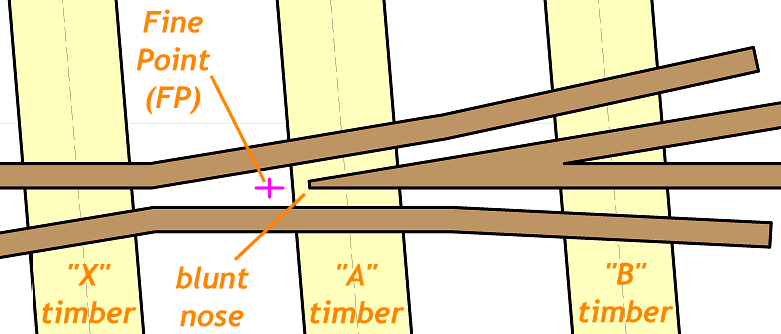 In the case of regular and generic V-crossing types the rails then continue at that angle through the vee rails and beyond. Even if the turnout is inserted in curved track, the relative displacement of the vee rails remains the same, i.e. the radius in both vee rails is the same. However, in the case of a curviform type of V-crossing, the angle applies only at the FP, and the rails of the diverging road beyond there continue to curve away from the main road at the same radius. This means that the angle between the vee rails increases as you move along them. Consequently, if a curviform V-crossing is inserted in curved track, the vee rails differ in radius. More about all this at: http://www.templot.com/martweb/gs_realtrack.htm Crossing angles are normally specified in unit angles, i.e. as a ratio such as 1:7 (sometimes written as #7, especially in the USA). There are two common ways of measuring the ratio: 1. RAM = Right Angle Measure = Templot default and some Continental European prototypes: ram_angle_diagram.png 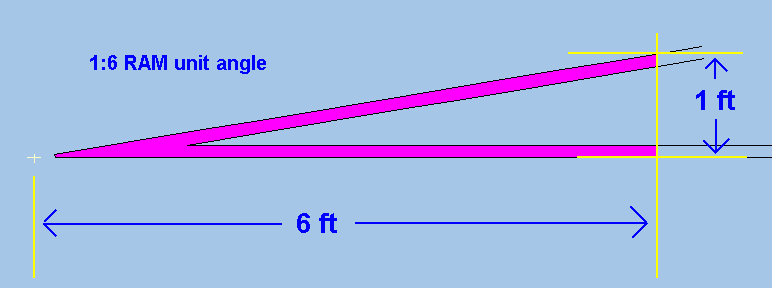 RAM unit angles are traditionally used by modellers because they correspond with normal engineering practice and are easily set out with dividers -- all measurements are either along the rail or at right-angles to it. Templot uses RAM angles by default for this reason. 2. CLM = Centre Line Measure = most US and UK prototypes: clm_angle_diagram.png 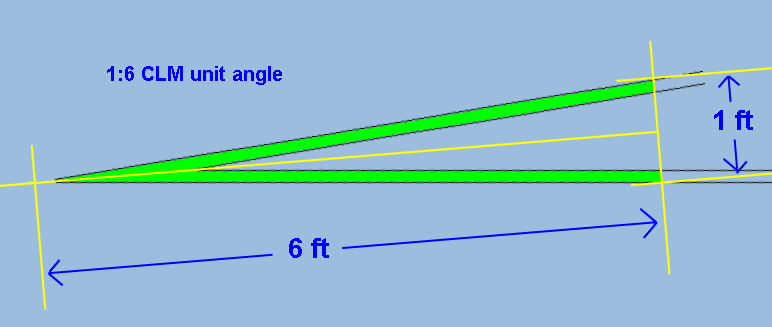 Measurements are made along an imaginary centre-line between the vee rails, and at right angles to that centre-line. Neither measurement is along the rail. It's easy to do on the ground with gauging tools which fit across the rails, but more difficult on a drawing board. CLM unit angles are used because the rules-of-thumb formulae which are used by the p.w. gang when setting out pointwork on the ground are simplified, and produce closer approximations to the true mathematical result. Nowadays with everything done on computers there is no real need for unit angles, we could work directly in degrees or radians. But tradition dies hard and the unit numbers are brain-friendly and easy to remember. regards, Martin. |
||
|
posted: 14 Feb 2013 07:50 from: CoBo
click the date to link to this post click member name to view archived images |
Thank you Martin | ||
| Please read this important note about copyright: Unless stated otherwise, all the files submitted to this web site are copyright and the property of the respective contributor. You are welcome to use them for your own personal non-commercial purposes, and in your messages on this web site. If you want to publish any of this material elsewhere or use it commercially, you must first obtain the owner's permission to do so. |